3 Vectores

3.1 Definición

Para definir un vector se utiliza la función c(), que siginfica combine

x <- c(1,2,6,90,76.7)

3.1.1 Longitud de un vector

Para obtener la longitud de un vector, es decir el número de elementos que tiene se utiliza la función length()

length(x)

## [1] 5

Como siempre, para mostrar el contenido de una variable sólo es necesario poner la variable y presionar enter en la sesión interactiva, si se está en un script es necesario usar la función print()

3.2 Uso de la función combine `c()` y el operador `:`

Un vector se puede definir de forma extensiva, es decir poniendo explícitamente todos los valores del vector.

y<-c("esto","es","un","vector")
z<-c(1,10,100,1000)

Esto es muy poco eficiente a menos que los vectores sean muy pequeños por lo que existen funciones para generar algunos casos particulares. Por ejemplo, si queremos tener un vector que tenga los primeros 100 números enteros podemos definirlo de la siguiente manera con el uso del operador : :

x<-1:100;
x

##   [1]   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
##  [19]  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36
##  [37]  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53  54
##  [55]  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72
##  [73]  73  74  75  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90
##  [91]  91  92  93  94  95  96  97  98  99 100

También se puede usar de forma equivalente la función seq() que significa sequence. seq() es una generalización del operador :,

x<-seq(1,100)
x

##   [1]   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
##  [19]  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36
##  [37]  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53  54
##  [55]  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72
##  [73]  73  74  75  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90
##  [91]  91  92  93  94  95  96  97  98  99 100

con ella podemos generar secuencias numéricas de distintas clase y espaciadas por diferentes rangos. Por ejemplo si queremos tener una secuencia de -12 a 30 en pasos de 3, es decir -12, -9,-6,…, 27,30 Teclearíamos

x<-seq(from=-12,to=30,by=3)
x

##  [1] -12  -9  -6  -3   0   3   6   9  12  15  18  21  24  27  30

Podemos omitir los nombres from, to,by si usamos el mismo orden, si queremos intercambiarlo debemos necesariamente ponerlos

y<-seq(0,1,0.1)
y

##  [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

z<-seq(by=0.1, to =1, from=0.5)
z

## [1] 0.5 0.6 0.7 0.8 0.9 1.0

3.3 Acceder a elementos de un vector

3.3.1 Elementos consecutivos de un vector

Para acceder a elemetnos de un objeto con índices en R debemos usar los corchetes [] para indicarle que queremos seleccionar esos objetos

x<-c("Muchos", "años" ,"después" ,",", "frente", "al" ,"pelotón")
x[1:4]

## [1] "Muchos"  "años"    "después" ","

x<-c(1,2,3,5,8,13,21)
x[3:6]

## [1]  3  5  8 13

3.3.2 Elementos no consecutivos de un vector

Para seleccionar elementos no consecutivos definimos un nuevo vector (con la función c() ) de índices que seleccionará los elementos que quieres

x<-c("Muchos", "años" ,"después" ,",", "frente", "al" ,"pelotón")
x[c(1,3,5,7)]

## [1] "Muchos"  "después" "frente"  "pelotón"

No es necesario que estén en orden

x<-c(1,2,3,5,8,13,21)
x[c(2, 7, 4)]

## [1]  2 21  5

3.3.3 Excluir elementos de un vector

Para seleccionar algunos elementos excepto un conjunto de ellos usamos el signo menos -

x<-c(1,2,3,5,8,13,21)
x[-2]

## [1]  1  3  5  8 13 21

# Todos menos el segundo elemento
x[-c(2, 7, 4)]   # Todos menos el segundo , séptimo y cuarto elemento

## [1]  1  3  8 13

x[-length(x)]    # ¿Esto qué hace?

## [1]  1  2  3  5  8 13

Este comando no elimina elementos de un vector sólo los selecciona

x<-c(1,2,3,5,8,13,21)
x[-6]

## [1]  1  2  3  5  8 21

x     # Estoy intacto

## [1]  1  2  3  5  8 13 21

3.4 Agregar y quitar elementos de un vector

x <- c(88,5,12,13)
x <- c(x[1:3],168,x[4]) 
x

## [1]  88   5  12 168  13

Podemos, incluso, definir un vector vacío y luego “llenarlo”

x<-c()
x                 # Soy un vector vacío :(

## NULL

x[1]<- 2
x[2:5]<-c(56,78,90,12)
x                 # Ahora ya no :)

## [1]  2 56 78 90 12

3.5 Repetición de elementos de un vector con `rep()`

La función rep() que viene del inglés repeat nos permite repetir elementos en un vector dado. Por ejemplo, rep(x,n veces)

x<-rep(3,5)
x

## [1] 3 3 3 3 3

y<-rep(c(1,2,3,5),3)
y

##  [1] 1 2 3 5 1 2 3 5 1 2 3 5

primos<-c(1,2,3,5,7,11)
z<-rep(primos,4)
z

##  [1]  1  2  3  5  7 11  1  2  3  5  7 11  1  2  3  5  7 11  1  2  3  5  7 11

También podemos usar la opción each para indicar la frecuencia de repetición

x<-c(1,2,3,4)
y<-rep(x,each=2)
y

## [1] 1 1 2 2 3 3 4 4

3.6 Uso de funciones `any()` y `all()`

Las funciones any() y all() determinan si alguno o todos los elementos de un vector cumplen cierta condición respectivamente. La respuesta siempre será un valor booleano es decir: TRUE o FALSE

x<- 1:15
any(x > 7.5)

## [1] TRUE

any(x > 19.76)

## [1] FALSE

any(x >= 15)

## [1] TRUE

all(x> sqrt(100))

## [1] FALSE

all(x>0)

## [1] TRUE

3.7 Operaciones con vectores

Al igual que en álgebra podemos definir varias operaciones que nos dejan siempre otro vector:

Suma (resta) de vectores
Producto de vectores (término a término)
Producto de un escalar por un vector

x<-c(1,2,3)
y<-c(4,5,6)
x + y

## [1] 5 7 9

x-y

## [1] -3 -3 -3

x*x

## [1] 1 4 9

y*y

## [1] 16 25 36

x*y

## [1]  4 10 18

3*x                #Multiplicación por escalar: término a término

## [1] 3 6 9

sqrt(2)*y          # Sí, por cualquier escalar!

## [1] 5.656854 7.071068 8.485281

3*x + sqrt(2)*y    # Operaciones más complejas

## [1]  8.656854 13.071068 17.485281

También podemos aplicar funciones para calcular con una sola instrucción varias operaciones útiles, por ejemplo min(), max(), range() , sum(), mean(), median(), sd(),quantile(),unique(),sort() Si tienes duda de qué hace alguna de ellas busca en la ayuda

x<-rnorm(1000)
min(x)

## [1] -4.390599

max(x)

## [1] 3.003573

range(x)

## [1] -4.390599  3.003573

sum(x)

## [1] -35.67603

mean(x)

## [1] -0.03567603

median(x)

## [1] -0.03247518

sd(x)

## [1] 1.01305

quantile(x)

##          0%         25%         50%         75%        100% 
## -4.39059910 -0.69384146 -0.03247518  0.67262680  3.00357310

Para unique() y sort() conviene tener elementos discretos más que continuos

x<- c(rep(3,5),1:15,rep(c(1,2,3),5))
unique(x)

##  [1]  3  1  2  4  5  6  7  8  9 10 11 12 13 14 15

x<-sample(10,10)
x

##  [1]  7  9  5  3  6  1  2 10  4  8

sort(x)

##  [1]  1  2  3  4  5  6  7  8  9 10

3.8 Gráficos con vectores

Podemos graficar los vectores de manera inmediata en R

x<- rnorm(10000)
hist(x,col="tomato2")

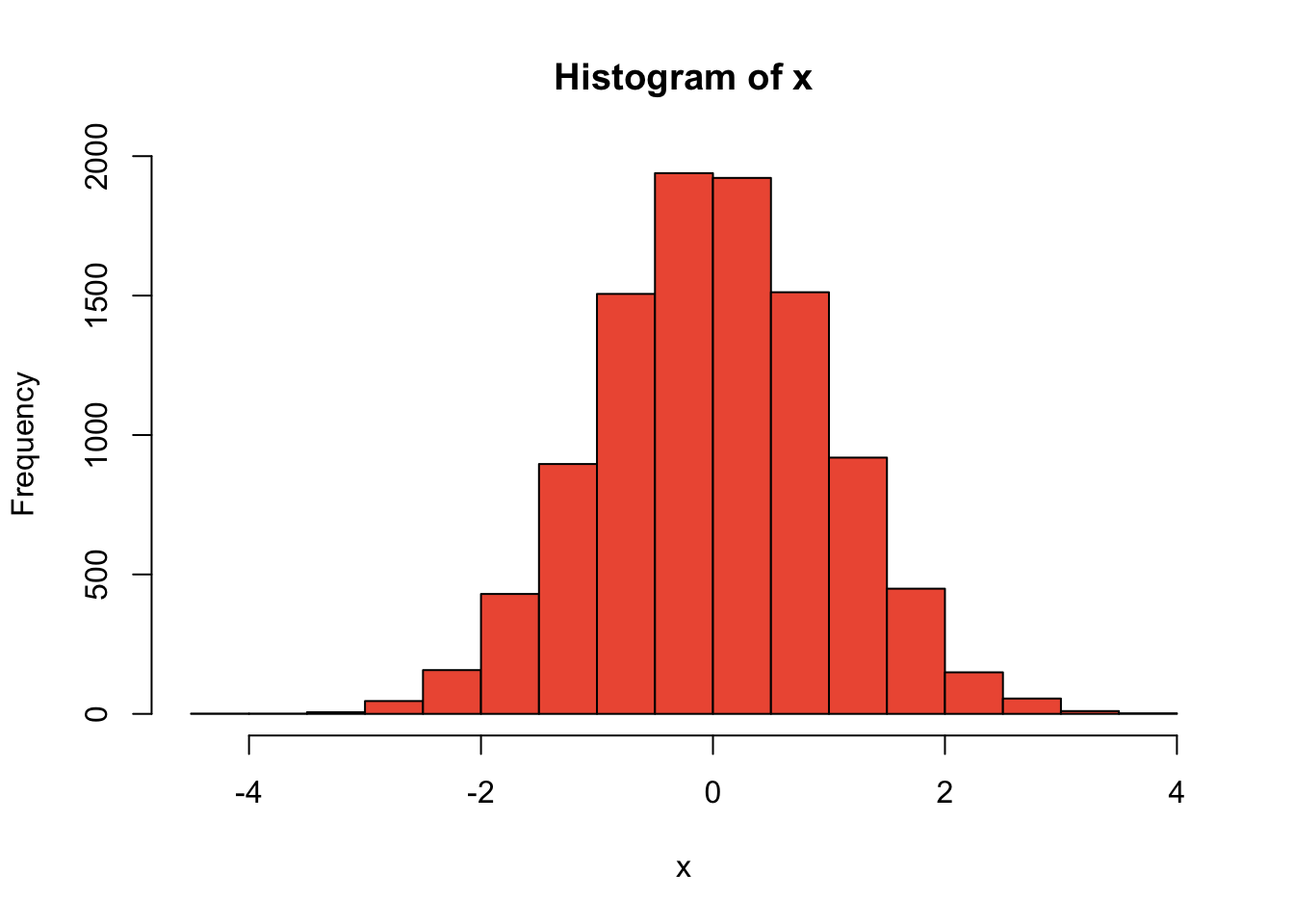
plot(x,col="salmon")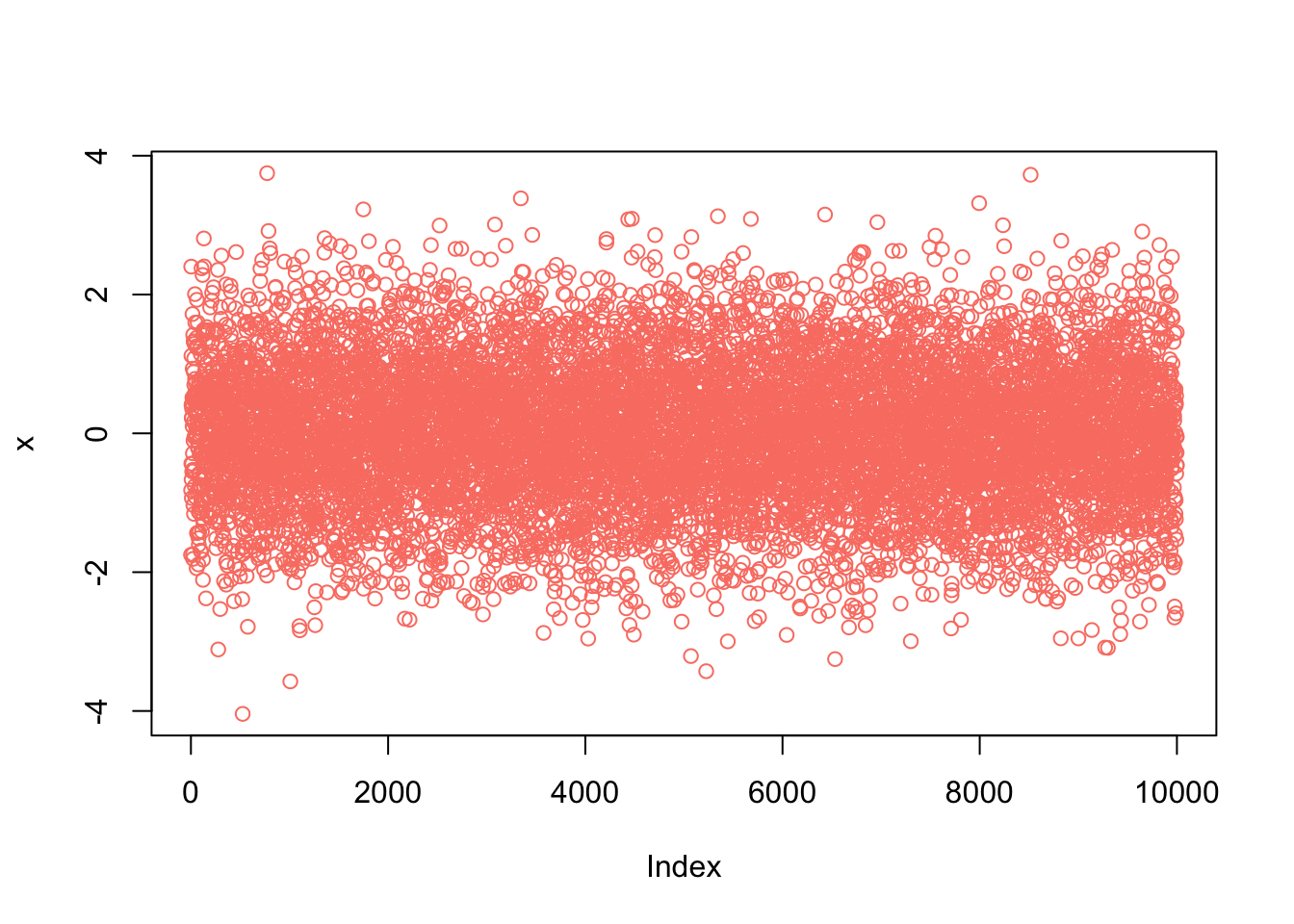

boxplot(x,col="wheat")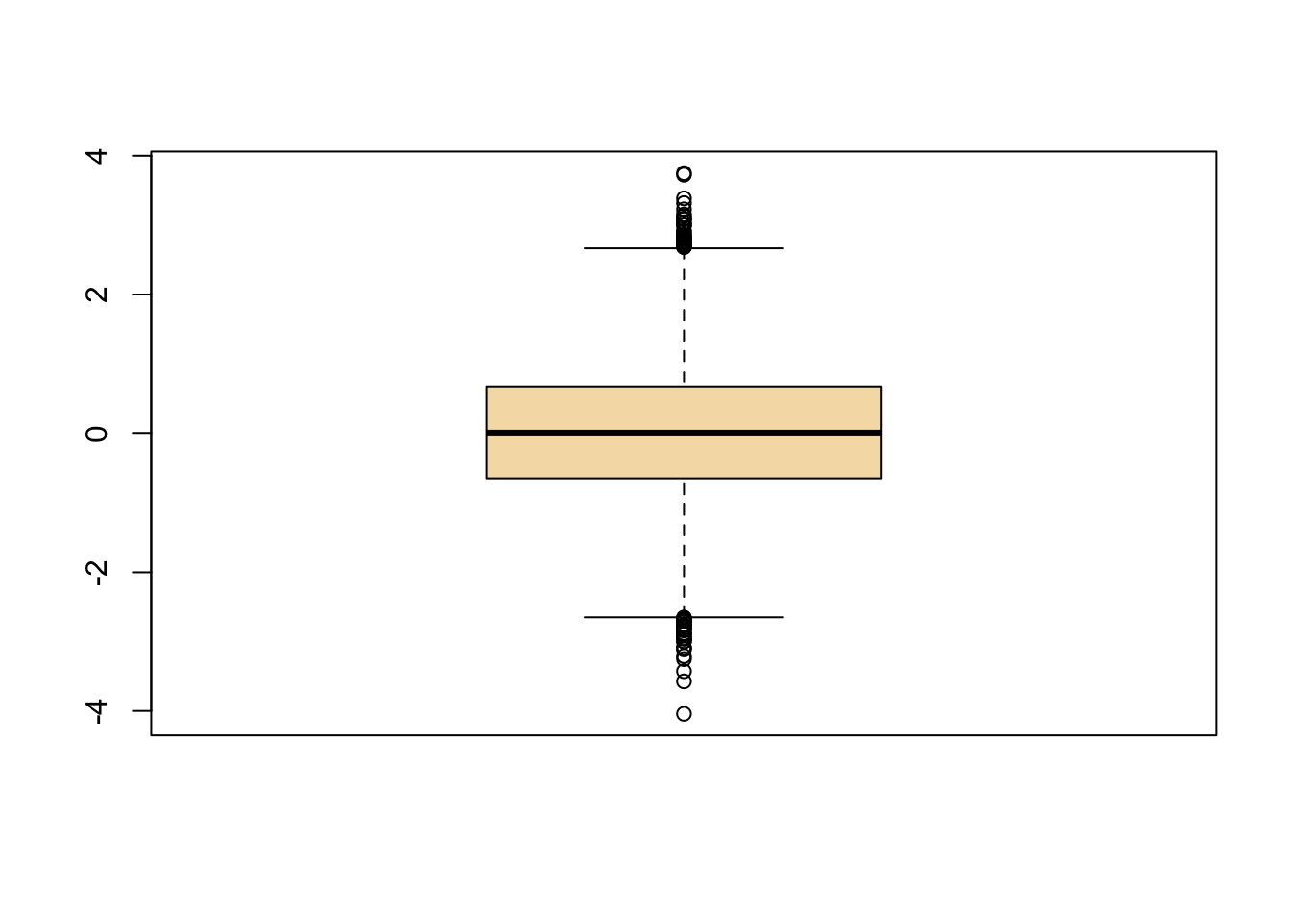

3.9 Vectores con nombre

Definimos un vector llamado edades

edades<-c(35,35,70,17,14)
edades

## [1] 35 35 70 17 14

Podemos definir un vector del mismo tamaño que edades llamado nombres

nombres <-c("Jerry","Beth","Rick", "Summer","Morty")
nombres

## [1] "Jerry"  "Beth"   "Rick"   "Summer" "Morty"

Una de las cracterísticas de R es que podemos asignarles nombres a los vectores, para ello usamos la función names()

names(edades)<-nombres

Con ello ahora el vector edades tiene una nueva característica:

edades

##  Jerry   Beth   Rick Summer  Morty 
##     35     35     70     17     14

Podemos selecccionar de la manera usual, por ejemplo, si quiero ver cuál es la edad de Rick, debo seleccionar el 3 elemento

edades[3]

## Rick 
##   70

Esto es muy poco eficiente y propenso al error sobre todo con vectores muy grandes. Por ello podemos usar los nombres de los vectores

edades["Rick"]

## Rick 
##   70

Recuerda que los nombres S-I-E-M-P-R-E van entre comillas

edades[c("Rick","Morty")]

##  Rick Morty 
##    70    14

Ejercicios:

¿Cuál es el promedio de las edades, sin contar el de Beth?
Quiten a Morty del vector, ordénenlo y guárdenlo como un nuevo objeto.
¿Hay alguna edad que sea mayor de 75? ¿Menor de 12? ¿Entre 12 y 20?

3.9.1 Tamaños de genomas

Ahora veamos un ejemplo más “biológico”

genomeSizeM_BP<-c(3234.83,2716.97,143.73,0.014281,12.1)

Por ejemplo si quisierámos ver el tamño en bp simplemente multiplicamos por el valor del prefijo Mega = 1 millón

genomeSizeM_BP*1e6

## [1] 3234830000 2716970000  143730000      14281   12100000

organismo<-c("Human","Mouse","Fruit Fly","Roundworm","Yeast")

names(genomeSizeM_BP) <- organismo

genomeSizeM_BP

##       Human       Mouse   Fruit Fly   Roundworm       Yeast 
## 3234.830000 2716.970000  143.730000    0.014281   12.100000

Se pueden seleccionar elementos de un vector utilizando corchetes

genomeSizeM_BP[1]

##   Human 
## 3234.83

Para obtener elementos consecutivos

genomeSizeM_BP[1:4]

##       Human       Mouse   Fruit Fly   Roundworm 
## 3234.830000 2716.970000  143.730000    0.014281

Para obtener elementos NO consecutivos

genomeSizeM_BP[c(1,2,5)]

##   Human   Mouse   Yeast 
## 3234.83 2716.97   12.10

Para selecciona (no eliminar, ni quitar) elementos excepto algunos

genomeSizeM_BP[-c(1,3,5)]

##       Mouse   Roundworm 
## 2716.970000    0.014281

Para referirnos a los elementos por su nombre

genomeSizeM_BP[c("Yeast","Human")]

##   Yeast   Human 
##   12.10 3234.83

Además de algunas operaciones aritméticas, se pueden calcular la media, máximo, mediana, mínimo, suma y longitud de los vectores

Ejercicio

Generar un vector de las edades de 10 de tus compañeros
Asignales nombre.
Encuentra el mínimo,máximo, media, mediana, la desviación estándar, la longitud del vector y selecciona sólo los elementos impares.
Elimina el máximo y el mínimo y con el vector resultante realiza un histograma.
Crea un vector de caracteres con diez nombres de especies y asocialo con su número de acceso de NCBI para su genoma en nucleótidos.

3.10 ¿Cómo lidiar con las NAs ?

Es (muy) freceunte que en bases de datos se tengan valores NA, es decir medidas que no pudieron realizarse, medidas perdidas, etc. Para ello se utiliza NA. R trata de manera especial a las NAs

x <- c(88,NA,12,168,13)

Existe una fución para determinar si un elemento es o no una NA. La función es is.na()

x <- c(88,NA,12,168,13)

is.na(x)

## [1] FALSE  TRUE FALSE FALSE FALSE

Si queremos calcular ciertas funciones numéricas R no sabrá qué hacer

x <- c(88,NA,12,168,13)
mean(x)

## [1] NA

Sin emabrgo, podemos decirle a R que las omita, indicando como argumento de la función mean() na.rm=TRUE que significa na remove

x <- c(88,NA,12,168,13)
mean(x,na.rm=TRUE)

## [1] 70.25

¿Qué otras funciones tienen esta opción?

3.11 Filtrado de elementos de un vector

Podemos generar vectores de que sean subconjuntos de vectores más grandes que cumplan cierta(s) condición(es)

un_vector<-c(1,2,3,5,7,11,13,17,19) 
otro_vector <- un_vector[un_vector*un_vector > 10]   # Leeme de adentro hacia afuera
otro_vector

## [1]  5  7 11 13 17 19

Veamos paso a paso qué es lo que hace este proceso

un_vector

## [1]  1  2  3  5  7 11 13 17 19

un_vector*un_vector > 10    # Mira, de adentro hacia afuera

## [1] FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

indices<-un_vector*un_vector > 10 
un_vector[indices]

## [1]  5  7 11 13 17 19

un_vector[c(FALSE,FALSE,FALSE,TRUE,TRUE,TRUE,TRUE,TRUE,TRUE)]

## [1]  5  7 11 13 17 19

la representación interna de los valores booleanos FALSE y TRUEson 0 y 1 respectivamente

un_vector[c(rep(0,3),rep(1,1))]

## [1] 1

3.11.1 Filtrado con `subset()`

Podemos usar la función subset()para hacer lo mismo que en el caso anterior excepto que omite los NA

un_vector<-c(1,2,3,5,7,11,13,17,19) 
otro_vector <- subset(un_vector,un_vector*un_vector > 10)   
otro_vector

## [1]  5  7 11 13 17 19

Qué pasa si tenemos NAs. Si usamos el método anterior obtendríamos

un_vector<-c(1,2,3,5,7,11,NA,13,17,NA,19) 
otro_vector <- un_vector[un_vector*un_vector > 10]   # Leeme de adentro hacia afuera
otro_vector  # Aquí salen las NAs

## [1]  5  7 11 NA 13 17 NA 19

En cambio con subset()

un_vector<-c(1,2,3,5,7,11,NA, 13,17,NA, 19) 
otro_vector <- subset(un_vector,un_vector*un_vector > 10)   
otro_vector  # Aquí ya no aparecen las NAs

## [1]  5  7 11 13 17 19

3.11.2 La función de selección `which()`

La función which() nos regresa los índices es decir nos dicen quiénes cumplen cierta condición

z <- c(5,2,-3,8)
which(z*z > 8)

## [1] 1 3 4

Acá nos dicen quiénes

z[which(z*z > 8)]

## [1]  5 -3  8

3.12 ¿Cómo podemos ver si dos vectores son iguales?

Dos vectores son iguales si elemento a elemento son idénticos. Por lo tanto deben de ser del mismo tamaño. Para probar si dos elementos son iguales se utiliza el operador de comparación == son dos signos iguales juntos, sin espcaio. No confundir con el operador = que se puede usar como operador de asiganción (aunque no es recomendable su uso. De hecho está prohibido en este curso)

x<-c(1,4,9,16,25)
y<-1:5
y<-y*y

x==y

## [1] TRUE TRUE TRUE TRUE TRUE

¿Qué pasaría si me confundo y escribo el operador de igualdad en lugar del de comparación?

y <-5:9
y

## [1] 5 6 7 8 9

x=y

## [1] 5 6 7 8 9

## [1] 5 6 7 8 9

Para vectores grandes puedo usar la función all() que ya vimos arriba

x <- seq(1,10000,1)
y <- seq(1,10000,1)
all(x==y)

## [1] TRUE

¿Cómo podríamos corrobar que son iguales usando any?

También podríamos utilizar que TRUE es 1 y que FALSE es 0

¿Por qué este código nos dice que sí son iguales?

sum(x==y)

## [1] 10000

3.12.1 Factor

Los factores son un tipo de vector que puede tomar un número “limitado” de valores, que normalmente se utilizan como variables categóricas. Por ejemplo: macho/hembra. Es útil tenener este tipo de objeto porque varios modelos estadísticos que se pueden correr en R los utilizan. A los valores que pueden tomar los elementos del factor se les conoce como levels.

x<- c(1,2,2,3,1,2,3,3,1,2,3,3,1)
x

##  [1] 1 2 2 3 1 2 3 3 1 2 3 3 1

as.factor(x)

##  [1] 1 2 2 3 1 2 3 3 1 2 3 3 1
## Levels: 1 2 3

x<-as.factor(x)
x

##  [1] 1 2 2 3 1 2 3 3 1 2 3 3 1
## Levels: 1 2 3

Los factores son una manera computacionalmente eficiente de almacenar caracteres, pues cada valor único (level) se guarda solo una vez y a los datos se les asigna un valor entero.

meses = c("March","April","January","November","January",
       "September","October","September","November","August",
        "January","November","November","February","May","August",
        "July","December","August","August","September","November",
         "February","April")
meses

##  [1] "March"     "April"     "January"   "November"  "January"   "September"
##  [7] "October"   "September" "November"  "August"    "January"   "November" 
## [13] "November"  "February"  "May"       "August"    "July"      "December" 
## [19] "August"    "August"    "September" "November"  "February"  "April"

meses<-as.factor(meses)
meses

##  [1] March     April     January   November  January   September October  
##  [8] September November  August    January   November  November  February 
## [15] May       August    July      December  August    August    September
## [22] November  February  April    
## 11 Levels: April August December February January July March May ... September

El que existan los levels permite realizar ciertas operaciones y manipular el contenido del factor.

table(meses)

## meses
##     April    August  December  February   January      July     March       May 
##         2         4         1         2         3         1         1         1 
##  November   October September 
##         5         1         3

levels(meses)

##  [1] "April"     "August"    "December"  "February"  "January"   "July"     
##  [7] "March"     "May"       "November"  "October"   "September"

levels(meses)[1]

## [1] "April"

levels(meses)[1]<-"Abril"
levels(meses)

##  [1] "Abril"     "August"    "December"  "February"  "January"   "July"     
##  [7] "March"     "May"       "November"  "October"   "September"

meses

##  [1] March     Abril     January   November  January   September October  
##  [8] September November  August    January   November  November  February 
## [15] May       August    July      December  August    August    September
## [22] November  February  Abril    
## 11 Levels: Abril August December February January July March May ... September

Ejercicio

Lee la ayuda de as.factor para determinar cómo crear un factor “ordenado”
Crea un vector con los meses en los que todas las alumnas del grupo cumplen años.
Aprovecha los levels para generar un objeto que guarde el número de estudiantes que cumplena ño cada mes.

Ejercicio

Genera un vector con el nombre de 10 virus
Asocia esos nombres con su número de acceso en NCBI
Genera otro vector que contega los tamaños en pb y los nombres
Determina cuáles son mayores de 300 bp
Asocia un subconjunto de vectores que sean mayores (menores a 300 bp) y mayores (mayores a 300 bp)
Haz un histograma con los tamaños de todos
Dibuja un boxplot con los tamaños de todos.Pon en el eje los nombres de todos.

2 Introducción a R

4 Matrices

3 Vectores

3.1 Definición

3.1.1 Longitud de un vector

3.2 Uso de la función combine c() y el operador :

3.3 Acceder a elementos de un vector

3.3.1 Elementos consecutivos de un vector

3.3.2 Elementos no consecutivos de un vector

3.3.3 Excluir elementos de un vector

3.4 Agregar y quitar elementos de un vector

3.5 Repetición de elementos de un vector con rep()

3.6 Uso de funciones any() y all()

3.7 Operaciones con vectores

3.8 Gráficos con vectores

3.9 Vectores con nombre

3.9.1 Tamaños de genomas

3.10 ¿Cómo lidiar con las NAs ?

3.11 Filtrado de elementos de un vector

3.11.1 Filtrado con subset()

3.11.2 La función de selección which()

3.12 ¿Cómo podemos ver si dos vectores son iguales?

3.12.1 Factor

3.2 Uso de la función combine `c()` y el operador `:`

3.5 Repetición de elementos de un vector con `rep()`

3.6 Uso de funciones `any()` y `all()`

3.11.1 Filtrado con `subset()`

3.11.2 La función de selección `which()`